정렬이란?
정렬은 데이터를 순서대로 재배열하는 작업이다.
정렬을 위해서는 사물들을 서로 비교할 수 있어야 하고, 비교할 수 있는 모든 속성들은 정렬의 기준이 될 수 있다.
순서에는 오름차순(ascending order)과 내림차순(descending order)이 있다.
정렬시켜야 할 대상을 레코드(record)라고 부른다. 또한 레코드는 여러 개의 필드(field)로 이루어진다.
예를 들어 경주마에는 번호, 이름, 키, 나이, 품종, 연락처 등의 속성이 있는데, 이들이 필드가 된다.
또한 이들 중에서 정렬의 기준이 되는 필드를 키(key) 또는 정렬 키(sort key)라고 한다. 결국 정렬이란 레코드들을 키(key)의 순서로 재배열하는 것이다.
정렬의 복잡도와 효율성에 따른 분류
알고리즘 및 정렬은 단순하면 비효율적이기 마련이다.
단순하지만 비효율적인 방법으로는 삽입 정렬, 선택 정렬, 버블 정렬 등이 있다.
복잡하지만 효율적인 방법으로는 퀵 정렬, 병합 정렬, 기수 정렬, 팀 정렬 등이 있다.
킷값의 비교를 사용하지 않는 정렬
기수 정렬, 카운팅 정렬 등은 대부분의 정렬 방법과 달리 레코드의 킷값을 비교하여 정렬하지 않는다.
이들은 빠르게 정렬할 수는 있지만 적용할 수 있는 킷값이 제한된다는 문제가 있다.
정렬 장소에 따른 분류
내부 정렬 : 모든 데이터가 메모리에 올라와 정렬 수행
외부 정렬 : 데이터가 너무 커 일부만을 메모리에 올려 정렬
안정성(stability)

동일한 킷값을 갖는 레코드가 여러 개 존재할 경우, 정렬 후에도 이들의 상대적인 위치가 바뀌지 않는 성질
그림 상에서, 같은 값일 때 주황 - 초록의 순서로 배치되어있는 블럭이 정렬 이후에도 주황 - 초록으로 배치가 되어야 안정성을 충족한다고 볼 수 있다.
안정성을 충족하는 정렬에는 삽입 정렬, 버블 정렬, 병합 정렬 등이 있다.
제자리 정렬
입력 배열 이외에 추가적인 공간을 사용하지 않는 방법
미니 퀴즈
2. 비교가 아닌 분배에 의한 정렬 방식에 해당하는 것은?
1. 퀵 정렬 2. 기수 정렬 3. 버블 정렬 4. 힙 정렬
정답 : 2
3. 삽입 정렬은 안정성을 충족한다 (O)
4. 병합 정렬은 제자리 정렬이다 (X)
기본적인 정렬 알고리즘
선택 정렬(selection sort)
오른쪽 리스트에서 가장 작은 숫자를 요소를 꺼내서 순서대로 출력하는 작업을 반복

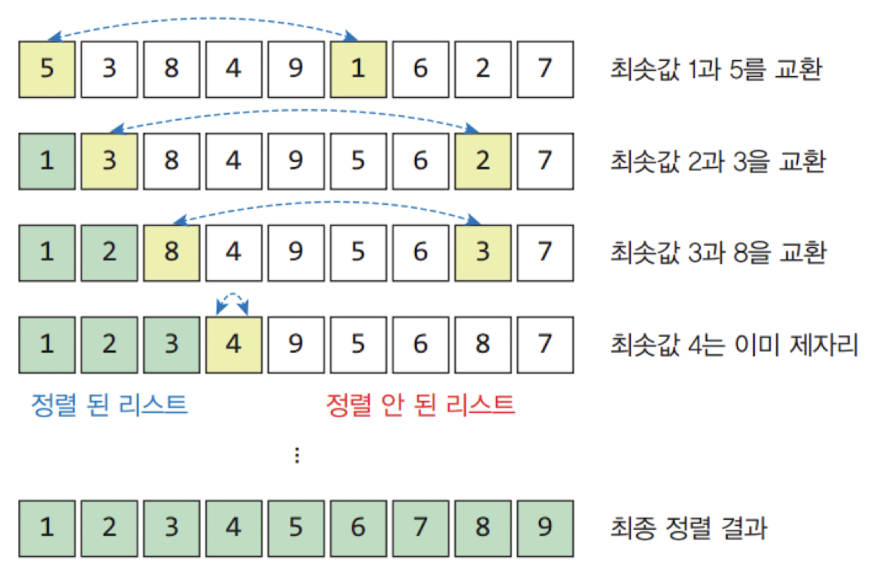
출력 배열이 추가로 필요할 수도 있지만, 최솟값이 선택되면 이것을 맨 앞의 요소와 교환하는 전략을 사용해 하나의 배열로 사용 가능하다.
알고리즘 코드
def selection_sort(A):
n = len(A)
for i in range(n-1):
least = i;
for j in range(i+1, n):
if (A[j] < A[least]):
least = j
A[i], A[least] = A[least], A[i]
printStep(A, i + 1)
#중간 과정 출력용 함수
def printStep(arr, val):
print(" Step %2d = " %val, end="")
print(arr)
실행 코드 및 결과는 다음과 같다.
data = [5, 3, 8, 4, 9, 1, 6, 2, 7]
print("Original : ", data)
selection_sort(data)
print("Selection sort : ", data)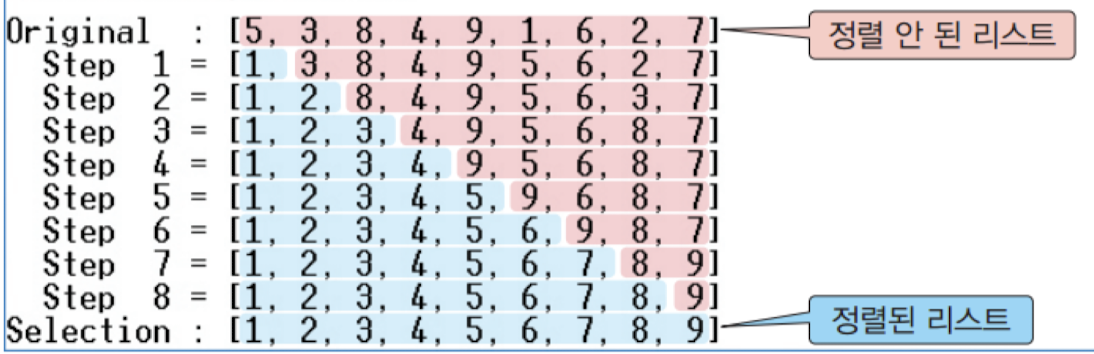
시간 복잡도
O(n^2) = (n-1) + (n-2) + ... + 1 = n(n-1)/2
결론
시간복잡도가 O(n^2)으로, 효율적인 알고리즘도 아니고 안정성을 만족하지도 않는다. 그러나 알고리즘이 간단하고, 입력 자료의 구성과 상관없이 자료 이동 횟수가 결정된다는 장점을 갖는다.
삽입 정렬 (insertion sort)
정렬되어 있는 부분에 새로운 레코드를 올바른 위치에 삽입하는 과정을 반복
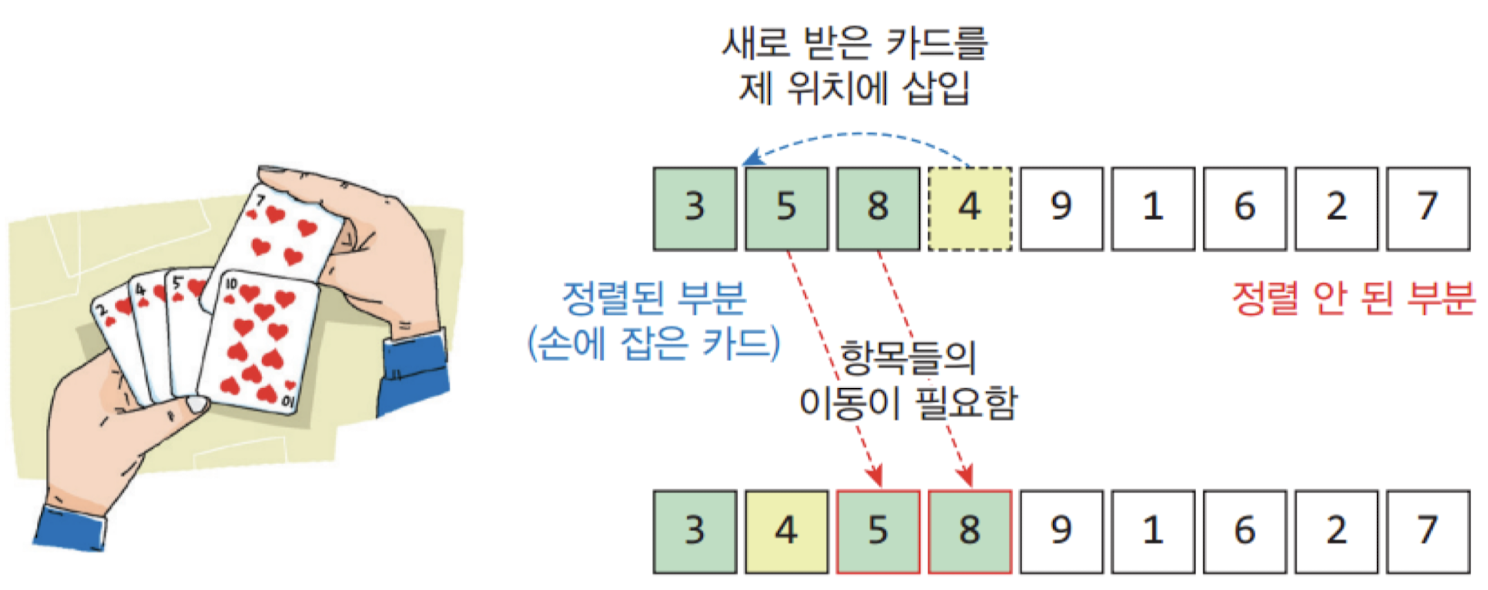
-> 숫자를 끼워넣기 위해선 많은 이동이 발생!

알고리즘 코드
def insertion_sort(A):
n = len(A)
for i in range(1, n):
key = A[i]
j = i-1
while j >= 0 and A[j] > key:
A[j + 1] = A[j]
j -= 1
A[j + 1] = key
printStep(A, i)
실행 결과는 다음과 같다.

시간 복잡도
최선의 경우 : O(n) -> 이미 정렬되어 있는 경우 : 비교 n-1번 수행
최악의 경우 : O(n^2) -> 역순으로 정렬되어 있는 경우
모든 단계에서 앞에 있는 자료 전부 이동
비교 : O(n^2)
이동 : O(n^2)
평균의 경우 : O(n^2)
결론
많은 레코드의 이동을 포함하므로 레코드가 크고, 양이 많은 경우 효율적이지 않다.
하지만 알고리즘이 간단하고, 안정성도 충족한다,
특히 대부분의 레코드가 이미 정렬되어 있는 경우 효율적으로 사용될 수 있다.
버블 정렬(bubble sort)
인접한 2개의 레코드를 비교하여 크기가 순서대로가 아니면 서로 교환
비교 - 교환 과정을 리스트의 전체에 수행
-> 한 번의 스캔이 완료되면 가장 큰 레코드가 리스트의 오른쪽 끝으로 이동
끝으로 이동한 레코드를 제외하고 다시 스캔 반복
더 이상 교환이 일어나지 않을 때까지 수행

알고리즘 구현
def bubble_sort(A):
n = len(A)
for i in range(n-1, 0, -1):
bChanged = False
for j in range(i):
if (A[j] > A[j+1]):
A[j], A[j+1] = A[j+1], A[j]
bChanged = True
if not bChanged: break;
printStep(A, n - i);
결과는 다음과 같다.
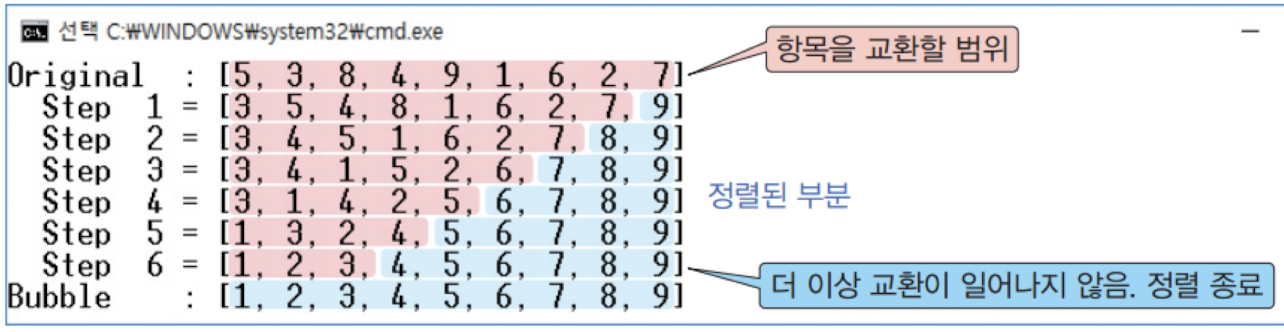
시간 복잡도
비교 횟수 = O(n^2) = n(n-1)/2
이동 횟수
- 역순으로 정렬된 경우(최악): 이동 횟수 = 3* 비교 횟수
- 이미 정렬된 경우(최선의 경우) : 이동 횟수 = 0
- 평균의 경우 : O(n^2)
기본적으로 이동 연산은 비교연산보다 더 많은 시간이 소요됨